Teaching Experience
I have served as a teaching fellow for an undergraduate class, Astronomy 16 - Stellar and Planetary Astrophysics, and for a graduate course, Astronomy 150 - Radiative Processes in Astrophysics. (These course websites need a Harvard PIN, but you can view the course description without a Harvard ID at in the Astronomy Department's Course Catalog). Both courses earned me a certificate of distinction in teaching, with Q-scores (based on student feedback) of 4.65/5 and 4.54/5, respectively.Below is an archive of my orginal teaching web page for Astronomy 16 (Fall 2009).
Astronomy 16 : Stellar and Planetary Astronomy
Spring 2009-2010
Dear Student,
On this page, you will find some thoughts relating to your
recent labs and problem sets in Ay16.
Hopefully, this page will help you build insight into problem-solving
in Physics and Astrophysics. If there is something specific you'd like
to talk about, write to me!
Five and a Half Steps to Solving a Numerical Problem
Here are some tips on solving numericals in Ay 16. These are not specific to this course. You may find these useful for solving problems in other courses in Physics and Astrophysics.
- Read the problem carefully. It is surprising how many errors in interpretation can be avoided just by this step alone.
- Make a list of (write down) all the data given to you.
- Write down what is asked in the question, i.e. make a list of the unknowns.
- What physics do you need to use? Write down the relevant formulae. What assumptions do you need to make? Justify them.
- Plug in the numbers, taking care to use a consistent system of units and using the appropriate number of significant figures.
It is strongly advisable to use scientific notation throughout. Do not leave units out of any number, unless you are feeling
particularly reckless.
Optional: convert your answer to friendly units - express masses of stars in solar masses, masses of planets in Earth or Jupiter masses, wavelengths in the visible spectrum in nanometers or angstroms, orbital radii of planets in AU, distances to stars in parsecs or light years ...
While this is usually not compulsory unless asked for specifically in the question, it puts your answer in context and makes it easier to interpret. Values for the sun's mass, the solar radius and other constants are usually provided with the question booklet, so you need not memorise them.
Finally - interpret your answers. Do you think they make sense, or is it obvious that you've made a mistake somewhere? If you have time, go hunting for errors by all means; but if not, make a statement about where you think you may have gone wrong, if you think that your answers look strange. And now that you have your numerical answer(s), check to see if your assumptions were valid. Hindsight, as they say, is 20/20. All the best for your final exam!
On the Significance of Significant Figures
All measurements and calculations have intrinsic errors and it makes no sense to quote an answer to ten significant digits when there is uncertainty in the second one. Besides, numbers with too many significant digits are hard to read and interpret. They also look ugly (there, I said it). Here are some tips regarding significant figures that you may find useful:
- How many significant figures should an answer have? Ideally a maximum of one more than the number of significant digits in the uncertainty for that answer, when written in scientific notation. So (5.67890 +/- 0.01) x 10-8 should be written as (5.67 +/- 0.01) x 10-8, because the uncertainty estimate (0.01 x 10-8) has TWO significant figures.
- When the uncertainty has not been calculated or is unknown, as is likely to be the case in any exam question, the number of significant figures in the final answer should be restricted to equal the number of significant figures in the least precise measurement used as input in deriving the final answer. For example, if the mass of a planet is 5.9742 x 1024 kg (five significant figsures) and its radius is given to be 6400 km (two significant figures), then its mean density, calculated to be 5440 kg m-3, should be quoted as 5400 kg m-3 or 5.4 g cm-3 to the correct number of significant figures (two).
- As a rule of thumb, keep ONE extra significant digit in all values during your calculation and round your final answer off to the correct number of significant digits at the end. Contrary to what you may think, keeping enormous numbers of significant digits in intermediate steps of a calculation will not improve your final accuracy in most cases. Copying out all those significant digits is not only a waste of precious time, especially in an exam, but puts you at a much greater risk of personal error (you may swap digits by mistake)!
Identifying Significant Digits
What are significant digits? Here are the relevant rules:
- All non-zero digits are significant.
- Zeros appearing between two non-zero digits are significant.
- Leading and trailing zeros are not significant in general, but trailing zeros to the right of the decimal point ARE significant
Exoplanet Challenge Checklist
Here are a few things you probably want to bring with you before you go up to catch that transit...
- Check the astronomical weather forecast!
- Check the time of astronomical twilight!
- Make sure your target is visible during the transit! The telescope has an elevation limit of about 20 degrees - so your target should be at a greater elevation than that THROUGHOUT the transit for you to be able to observe it. Remember - lower elevations also mean greater atmospheric air masses to look through! (Why is that bad?) To see if your target will be visible, use a planetarium software such as Stellarium or use an online coordinate converter. When in doubt, check the Julian Date.
- Print out finding charts for all of your targets! Note that the CCD footprint on the sky is 13 arcminutes on a side.
- Warm clothing: gloves and hats.
- Food! Don't be caught without some'n.
- A flashlight (preferably covered with red cellophane). There may be some in the dome, but plan to bring your own.
- Lots of patience. Things can and probably will go wrong. Keep a cool head and call someone if you see aliens approaching.
Happy Observing!!
Steps for Photometry for the Exoplanet Challenge
Here are the steps you would need to perform to carry out photometry with MaxIm DL. (Thanks to Allyson!)
CCD - Sequence mode
After you find your object, focus and find the right exposure time, you will want to set up a sequence of exposures. Make sure you are in autodark mode. This will automatically take the dark and subtract if from the images. Once you are ready to start taking the images, click on the "sequence" tab in the CCD control window. You will then be able to give a filename(i.e. OBJ_DATE_FILTER_EXP_). It allows you to set a start number and how many images to take. It will increment your images _1,_2 etc. The next important things is to remember to "set the path" (where you want to save your images). Again, save all images to Shared Docs on Thuban > Ay16_2010 > your folder. There is a button above set path called "setup" that allows you to input the exposure time, image type (Light) binning etc. THIS is where you input the exposure time when doing the sequence, NOT in the "exposure" tab. Then you hit the start button and are ready to go. For consistency, turn off all the red lights and the monitor in the dome when taking the images.
You can now go down to the lab (but keep an eye on the weather if its iffy) and start the analysis.
Photometry
First open all your images in Maxim DL. Look through all of your images to make sure you don't have any bad images (i.e. plane streaks etc).
To combine flats
- From top Pulldown menu - "process" > "set calibration" (this opens a new window).
- Next to the "add group" button change "Auto" to "Flat" and then click "add group".
- Under "combine type" change to median.
- Click "add" on bottom right and select all of your flat files from your directory.
- Click OK.
- Then in the top pulldown menu "process" > "calibrate all"
To do the photometry
With all images loaded.
- From top pulldown menu "Analyze" > "photometry" (this pops up a new window).
- Make sure "act on all images", "use star matching" and "Snap to centroid" are all checked (on bottom right of the new window).
- If you right click on your image you can change your aperture radius, gap width and annulus radius to the appropriate size.
- In photometry window, "under mouse click tag" there is an option for reference star, select it and click on a reference star in your image, enter its magnitude in the "ref mag" box - do this for as many ref stars you have.
- Then under "mouse click tag" you can choose "new object" and then click on the target.
- Finally, click on "view plot" and you will literally see the light curve. You can (just as in solar lab) click on "save" and save the file as a .csv / Excel file.
Taking flats
There is a tab in the telescope operation notebook that talks about sky flats. Remember to use "autodark" and to move the telescope (use the handpaddle and tap the "set" and "W" slightly) in between exposures. You literally just want to move the telescope a tiny amount in case stars appear in your images. As long as they are in different places, they will combine out. The important part is to try to do this quickly as the sun is setting and get a consistent amount of counts in your images (~20,00-30,000). 10 flats is probably enough, but it's your preference.
Binary Stars Lab: Measuring Stellar Radii
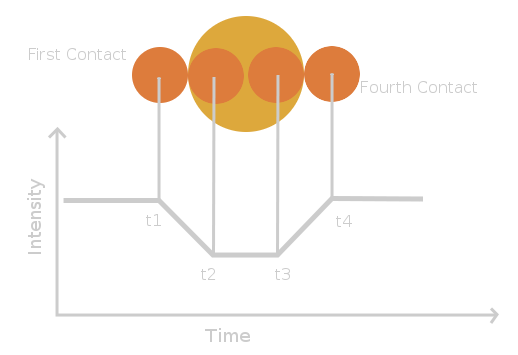
How do we measure the radii of stars from the shape of the light curve? During the lab, I wrote down a formula for the radii as determined from the light curves:
This formula is an approximation, where we have assumed that the stars are moving tangentially across our line of sight all through the eclipse. However, if the stars are physically close to each other and the transit time is a substantial fraction of the total orbital period, this may not be true. Below I derive this formula, first assuming that the stars are passing tangentially across the line of sight, followed by the correction for circular orbits.
Consider two stars with masses m1 (green) and m2 (red), sizes R1 and R2, orbiting the center of mass in circular orbits of radii a1 and a2 at orbital speeds v1 and v2 with a period, P. Let us assume this system is an eclipsing binary, with the angle of inclination of the orbit exactly 90 degrees, i.e. the orbit is exactly edge on and the centers of the stars line up in mid-eclipse.
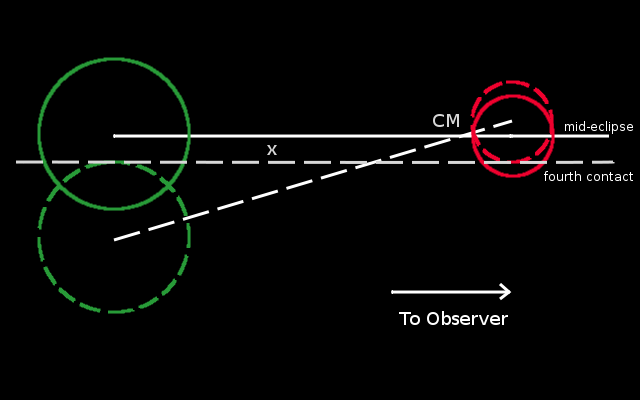
Consider the instant of mid-eclipse. This situation is drawn with the two stars shown in solid outline above. Since the light curve is symmetric about the minimum (time of greatest eclipse - when the centers line up), this happens at time tmin = (t1 + t4)/2, midway between the first and fourth contacts (which is the same as midway between the second and third contact). In this diagram, star 1 (on the left) is moving downwards, while star 2 (on the right) is moving upwards.
The Approximate Formula
Let us begin by assuming that the duration of the eclipse is much smaller than the orbital period. In this case, the stars move along straight lines (not shown), straight down (for star 1) and straight up (for star 2) over a time, t1/2 = t4 - tmin until the point of fourth contact, where t1/2 is half the total duration of the eclipse. The point of fourth contact is indicated above, with the stars shown in dashed outline. The dashed horizontal line denotes the line of sight for an observer far to the right, far off the plot. (Note: We can place the Line of sight wherever we like, parallel to the horizontal axis, since the orbital separation of the stars would be negligible compared to their distance from us).Let the physical separation between the lines of sight at mid-eclipse and at fourth contact be, x. Then we see that the center of star 1 moves a distance R1 + x in time t1/2, moving at speed v1, while the center of star 2 moves a distance R2 - x in the same time, t1/2, moving at speed v2
An Exact Formula For Short-Period Binaries
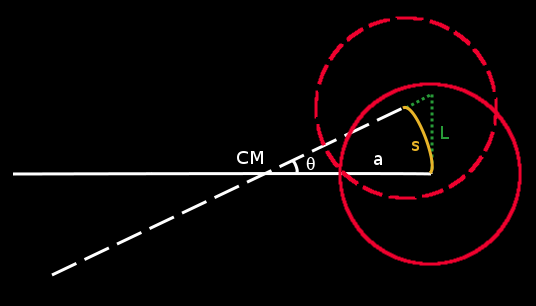
Consider star 2. From mid-eclipse to fourth contact, the center of the star traces the yellow arc, s:
The projection of this arc in the plane of the sky is shown by (the vertical segment of) the green dotted line. This is the distance the center of the star appears to move in the sky over a time t1/2 and has a length, L = R2 - x.
Since this forms one side of a right-angled triangle, we have:
For circular orbits, we also have:
 ,
,
Note that in the limit t << P, this reduces to the original approximate formula assuming tangential motion that we derived above, always a good sanity check! The leading order correction term (by expanding the tangent in a Taylor series) gives about a 40% (!) correction for our system. This effect is really important!
Finally, note that the formula for the radius of the smaller star, also derived in the lab
 ,
,
Lunar Recession
The Observation
It has been determined from lunar radar ranging experiments that the moon is slowly receding from Earth at about 3.8 cm/year. The cause of this has been linked to Earth's tides - differential acceleration by the moon on the Earth's oceans raises tides both in the oceans and in Earth's crust. Since Earth rotates faster than the moon revolves around Earth, Earth's tidal bulge leads the moon. The bulge in turn exerts a gravitational tug on the moon, pulling it forward in its orbit, making the moon climb higher and away from Earth.The Paradox
What is happening to the moon's orbital speed? Since it is being pulled ahead in its orbit, it is natural to think that it is being sped up. However this is not true. The moon is actually slowing down as it moves to higher orbits. This is the paradox of Keplerian orbits - higher orbits have smaller orbital speeds!The Mathematics ...
Consider a body moving in circular orbits about another, more massive body (such as Moon around Earth, or the planets around the Sun). The centripetal acceleration required to keep the smaller body in a circular orbit is provided by the gravitational force:

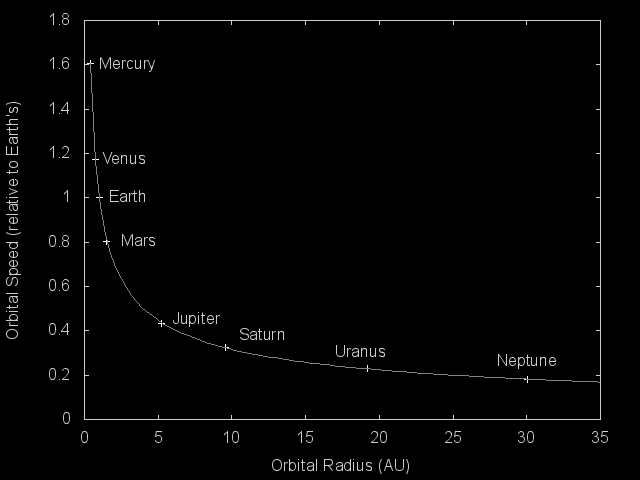
The orbital speeds versus mean orbital separation of the planets in the Solar System (scaled to Earth's orbital speed and distance from the Sun). The smooth curve is a plot of 1/sqrt(x).
The Physics
Why is it that our intution fails? The key is to look at the energy of the orbit. As the moon is dragged forwad in its orbit, it gains energy and it climbs out of Earth's gravitational potential well.
The total energy of the moon in its orbit,
Substituting for the speed, v from above, we have:
Now let us see how this orbital energy changes with time:
Let us now see what happens to the angular momentum of the moon in its orbit.
We have: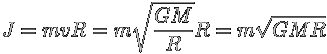
So its rate of change,
 (if dR/dt > 0)
(if dR/dt > 0) Therefore we see that as the moon recedes from Earth, it picks up energy and angular momentum, but it slows down in its orbit. Where does this energy and angular momentum come from? The answer is: from Earth's spin! As the moon moves away, the Earth's spin slows down. This is a measurable effect: the days are getting longer by about 0.0017 seconds per century!
As a final point, note that this will stop once Earth and Moon are both tidally locked to Eath other. This will happen when Earth's rotation period has grown from the present value of 1 day to about 47 days, and the moon's orbital period has also grown to match. Our science fiction writer was not quite right - the moon will never escape Earth's gravity and float off into space...
The Free Electron Gas
Fermions and Bosons
All fundamental particles have a property called the intrinsic spin angular momentum. Particles with a spin of half, or odd integer multiples of one half (i.e. 1/2, 3/2, 5/2 and so on) are said to be Fermions and follow the Pauli Exclusion Principle. Protons, neutrons and electrons are examples of Fermions. (You can actually prove that any particle with a spin that is an odd integral multiple of one half must follow the Exclusion Principle). Particles with spins that are even multiples of one half (i.e. 1, 2, 3 and so on) are called Bosons. The quantum of light energy, the photon, is an example of a Boson.Fermion Spin Degeneracy
Electrons are Fermions with a spin of one half, which means that a given electron can have two orientations of its spin with respect to a chosen axis (parallel or anti-parallel). This enables us to distinguish two electrons on the basis of their spin. This also allows two electrons to occupy the same quantum state without violating the Exclusion Principle, provided they have opposite spins. This is the reason why the lowest energy state in Hydrogen has a degeneracy factor of 2. It corresponds to the different spin states of the electron with respect to that of the nucleus. (Actually, the two states do not quite have exactly the same energy because of coupling of the electron's spin with the magnetic moment of the nucleus. This is called hyperfine splitting and is observable).
The above is true for any quantum mechanical state, not just inside an atom: any energy level will have a degeneracy of at least 2 because the electron that occupies it can have either spin, and is distinguishable based on its spin.
The Electron in a 1-D Box
Let us say we have a one-dimensional box with one electron. The electron is free to roam around inside the box, but it cannot leave the box. How we go about making such a box is described in the subsection "Free Electron Gases in Real Life", so hang in there! Les us say that the box has a total width, L. Then quantum mechanics tells us that there are various possible states the electron could be in, much like the states in an atom. If the electron has a momentum p, then it has a quantum mechanical wavelength, a.k.a. the de Broglie wavelength (see section 3.3.2 in Astronomy, A Physical Perspective), given by:
 , where h is Planck's constant.
, where h is Planck's constant.
Just like in an atom, the allowed states for the electron inside the box
are those for which there are an integral multiple of half de Broglie wavelengths inside the box.
In other words, the size of the box,
Why is there this factor of half, you ask? Well, ever plucked a guitar string in the middle? It starts oscillating in what is known as the fundamental mode, with maximum amplitude in the middle of the string and zero amplitude (called a node) at the two ends. In this mode, the wavelength of the oscillation of the guitar string is twice the length of the string. Therefore the string follows the above relation, at least for n = 1.
You can prove that the allowed modes on the string actually follow the above relation for all n (see the link). An electron in a box is like a standing wave on an oscillating string in that it follows the same relation between wavelength and box size as the string. This actually comes from solving Schrödinger's equation for the single electron in the box, which we will not attempt to do here.
Now that we have an expression for the wavelength of the electron, we equate this to the expression for the
de Broglie wavelength in terms of the momentum of the electron to obtain:
Therefore the energy of the (non-relativistic) electron,
where m is the electron mass.
We see that the energy levels for a single electron in a 1-D box are given by a single quantum number, n. Note that the energy in the non-relativistic case described here depends on the square of the momentum, not on the momentum itself.
The Electron in a 3-D Box: Degenerate States
Now consider the electron to be inside a 3-dimensional box cubical box of side, L. In general, the momentum of the electron would have three components corresponding to the three directions of space inside the box. We can write this as
Each of these momenta would be quantized:
where ![]() and
and ![]() are integers.
This gives us for the total energy:
are integers.
This gives us for the total energy:

Therefore the total energy of a single (non-relativistic) electron in a 3-D box depends on three quantum numbers,
![]() and
and ![]() . Note that there are combinations of
. Note that there are combinations of ![]() and
and ![]() that yield
the same energy, such as
that yield
the same energy, such as ![]() and
and ![]() .
States like these that are physically distinct but have the same energy are said to be degenerate states.
.
States like these that are physically distinct but have the same energy are said to be degenerate states.
Finally, note that each of these states with a given value of ![]() and
and ![]() is itself degenerate
with a degeracy of 2, because of the two possible spin orientation of the electron that occupies it.
Putting it all together, the lowest energy state, which has an energy of
is itself degenerate
with a degeracy of 2, because of the two possible spin orientation of the electron that occupies it.
Putting it all together, the lowest energy state, which has an energy of ![]() has an overall degeneracy of 2 (from spin) x 3 (from different values of
has an overall degeneracy of 2 (from spin) x 3 (from different values of ![]() and
and ![]() ) = 6.
The next higher state has energy
) = 6.
The next higher state has energy ![]() also has a total degeneracy of 3 x 2 = 6
corresponding to
also has a total degeneracy of 3 x 2 = 6
corresponding to ![]() = { (1,1,0), (1,0,1), (0,1,1) } (three distinct states) and
the factor of 2 from spin degeneracy.
= { (1,1,0), (1,0,1), (0,1,1) } (three distinct states) and
the factor of 2 from spin degeneracy.
An energy level that corresponds to many different (degenerate) states is said to be a degenerate energy level.
This energy level is said to have a degeneracy factor, g given by the number of states with that commmon value of energy.
In the Hydrogen atom, for example, the degeneracy factor, g is given by ![]() , where n is the principal quantum number.
, where n is the principal quantum number.
The Free Electron Gas
Now consider what happens if you put more electrons into the box. "Well, they start repelling each other", you will say. That is true. However, let us ignore that for a moment. "Why? How?!" I can here you exclaim. Well, I will justify it in the next section. Instead of considering the inter-electronic interactions, we will assume that the single-particle states whose energies we calculated above, are maintained even when we have more than one electron in the box and that the new electrons simply go in to fill up more higher-momentum states. It turns out that this is a good approximation for many systems, including metal objects such as the copper that a penny is made of! Such a system is know as the "free electron gas", free because the electrons are not interacting with each other or anything else (except for the walls of the box).
Let us now define what we mean by the "ground state". The ground state of a system corresponds to the state which has the lowest possible energy. This corresponds to a configuration of all the particles in the system such that together they minimize the total energy of the system. How on Earth are we going to compute that? Well, with our simplifying assumption that the electrons in a box behave as a free gas, this is really straighforward:
The first 6 electrons go into the 6 degenerate states with energy ![]() .
So if there are only 6 electrons in the system, then the total energy would be 6 times the energy of
the lowest energy state available to the electrons, i.e.
.
So if there are only 6 electrons in the system, then the total energy would be 6 times the energy of
the lowest energy state available to the electrons, i.e. ![]() .
The next energy level with energy
.
The next energy level with energy ![]() also has a degeneracy of 6,
so the next 6 electrons will go into those 6 states, giving us a total energy of the first 12 electrons to be
also has a degeneracy of 6,
so the next 6 electrons will go into those 6 states, giving us a total energy of the first 12 electrons to be
![]() .
The next level corresponds to
.
The next level corresponds to ![]() . There is only one such state, so it can hold two electrons.
Putting these in, we are up to 14 electrons with a total system energy of
. There is only one such state, so it can hold two electrons.
Putting these in, we are up to 14 electrons with a total system energy of
![]() .
.
This is fun! The next state has ![]() . It has a total degeneracy (including spin) of 6. So electrons
number 15 to 20 go there, giving us a total energy of
. It has a total degeneracy (including spin) of 6. So electrons
number 15 to 20 go there, giving us a total energy of ![]() .
We can go on like this, putting the electrons in the lowest energy level available to them, until we have used up all the electrons.
The highest energy level occupied by an electron in the gas is then called the Fermi energy,
.
We can go on like this, putting the electrons in the lowest energy level available to them, until we have used up all the electrons.
The highest energy level occupied by an electron in the gas is then called the Fermi energy, ![]() .
.
So far, we have the following:
| Total Number of Electrons, N |
Fermi Energy, in units of |
|---|---|
| 1 to 6 | 1 |
| 7 to 12 | 2 |
| 13 or 14 | 3 |
| 15 to 20 | 4 |
It is a little tedious to calculate these numbers exactly for a large number of electrons, so people resort to approximations involving the concept of phase space. We won't go into that here, but the basic phsyics remains what we have outlined above. The final formula for the Fermi energy for large numbers of non-relativistic electrons, N in a volume, V is:
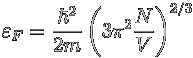 .
. Free Electron Gases in Real Life
So why do we care about electrons in a box? The reason is that many systems can be described by assuming that the electrons in them form a free Fermi gas, just like the one described above. The best example is that of metals at room temperature. Consider a block of copper (say a penny). Each atom of copper has one loosely bound outer electron that it can contribute to the greater good. So when atoms of copper sit down together in the crystal lattice of copper, they each donate an electron to the firmament and become positively charged.
Clearly, there are as many free electrons floating about as there are copper ions in the crystal. Together these electrons form a large, crystal-wide sort of chemical bond that keeps the copper atoms together in their crystal lattice and prevents the ions from flying apart from their mutual electrostatic repulsion. This is the so-called metallic bond. If we apply electric fields to the copper in the form of a voltage across the two sides of the penny, for example, the electrons start swimming in one direction (on average) and form a current. This is what gives metals their electrical conductivity.
These liberated electrons form a sea (called the Fermi sea) and are essentially free - they are not bound to any particular atom and roam about the entire crystal like a swarm of fish. However, no electron can escape the penny, because that would leave the penny positively charged, which would quickly attract the errant electron back. In other words, there is a strong opposing potential at the edges of the box, preventing the electrons from escaping. This is called the work function, and the study of this and the photoelectric effect earned Einstein the Nobel Prize. We see that the elctrons behave like they are trapped in a box - but inside the box they are free to move wherever they like. Therefore they form exactly the free electron gas we talked about above and the entire discussion in the above section carries over.
We can now calculate the Fermi energy (the highest energy level occupied by an electron in the system, see above) for a block of copper,
assuming that the electrons are all sitting in the lowest possible energies allowed to them, as described in the discussion on the Fermi gas.
The Fermi energy for this system turns out to correspond to a temperature of
about ![]() , where k is the Boltzmann constant.
Since this is much less than room temperature, this means that the excitations of electrons above the Fermi level is very small.
In other words, the majority of electrons do sit in the lowest allowed states possible, and our theory is self-consistent.
(Those electrons that do get excited give the copper its heat capacity, but that's another story).
The electrons in the Fermi Sea fill up the allowed energy levels bottom-up, two at a time as described above, up to the Fermi energy.
The entire metal is in a collective ground state (note for the aficionados: this is only strictly true at absolute zero temperature).
The electron gas is said to be strongly degenerate.
A similar sort of thing happens in white dwarf stars and is described in the next section.
, where k is the Boltzmann constant.
Since this is much less than room temperature, this means that the excitations of electrons above the Fermi level is very small.
In other words, the majority of electrons do sit in the lowest allowed states possible, and our theory is self-consistent.
(Those electrons that do get excited give the copper its heat capacity, but that's another story).
The electrons in the Fermi Sea fill up the allowed energy levels bottom-up, two at a time as described above, up to the Fermi energy.
The entire metal is in a collective ground state (note for the aficionados: this is only strictly true at absolute zero temperature).
The electron gas is said to be strongly degenerate.
A similar sort of thing happens in white dwarf stars and is described in the next section.
Degeneracy Pressure
From the model of the free electron gas, a pressure can be computed. This turns out to be:
White Dwarfs
There appeared to be much confusion in the reading questionnaires about the cause of degeneracy pressure in white dwarf stars. First of all, note that the gas deep inside a star is completely ionized. In other words, at the temperatures of stellar cores electrons are no longer bound to the atoms and form a soup of negative charge floating about amidst a sea of positive ions (atomic nuclei). The positive ions give the plasma overall charge neutrality. (If the plasma were not charge neutral as a whole, say if it were made only of electrons, it would fly apart because the electrostatic force is so much stronger than the gravitational force!) This is similar to the case of the metal above, with the electrons forming a free Fermi gas. The Fermi energy (divided by the Boltzmann constant) of the free electron Gas in White Dwarf stars is also much higher than their physical temperature. This is why white dwarf matter can be treated as a solid by analogy with the case of a metal at room temperature.
That brings us to the question in the section "The Free Electron Gas" that I promised I would answer later, namely why can we ignore the interelectronic repulsion? The first reason is that this repulsion is partially screened by the presence of a background of positive charge. An electron on average feels the effect of the net charge around it, which can fluctuate, but would be zero on average.
The second reason is a little deeper and has to do with the fact that the electrons must occupy some quantum level or other. An interaction of the electrons can be modelled as a collision and the effect of the interaction then is the exchange of a bit of momentum between them. The constraint is that they must occupy some two energy levels before the collision and some different energy levels after the collision. This means that the participating electrons get scattered from one state to another. This can happen only when there are empty states for the electrons to get scattered into.
However, all the states inside the Fermi Sea are filled, as we discussed above - so there are no free states for electrons deep within the Fermi Sea to get scattered into. They can scatter into very high energy states, above the Fermi Sea, but that would involve a very large change in their momentum, so such collisions must be rare. Of course, electrons near the top of the Fermi Sea can easily scatter into the states above the Sea, which are close to their original energy. But these electrons near the surface of the Fermi Sea form a minority of the total population; most of the electrons reside in the bulk.
These reasons, then, tell us why our theory works. In fact, it is remarkably good at predicting the properties of both white dwarf stars and copper pennies. Another example of the versatility of Physics (and Astrophysics!)
Error Analysis (Fractional errors)
No scientific measurement is complete without an estimate of the errors. While there are several sources of error in a measurement, we will not go into those here, and instead talk about how errors in one quantity effect the errors in a derived quantity, a topic known as error propagation.
Let us say you can measure the temperature of star using spectroscopy (say using Wien's law) as T ± ΔT, where ΔT is the uncertainty in the temperature measurement and that you also measure the distance to the star, say using parallax as D ± ΔD. Finally, say that you can also measure the total flux from the star received at Earth as F ± ΔF. Given these quantities, what is the luminosity of the star?
We have the formula:
To determine the fractional error in the luminosity, we take the logarithm of the above equation and then take differentials:
Say you now want to find the star's radius, knowing also its temperature.
You decide to use the Stefan-Boltzman law:
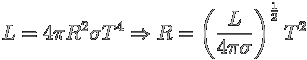
What is the error in the radius that you determine? Again, taking logarithms and then differentials, we have:
Notice that this is due to the strong dependance of the luminosity on the temperature, and the somewhat weaker dependence on radius. In general, if a quantity, Y you are trying to measure has a strong dependence on someother quantity, X, then it is really important to measure X as accurately as possible. Think about what quantities appear with strong dependances in the final formula for the AU in the solar lab. What are the sources of error in their measurement? Also think about how you can go about reducing the error in the measurement of these quantities.
Finally, keep in mind that the description of error propagation presented here is relatively simple-minded. It provides a conservative estimate of the errors. The true errors are usually smaller than those estimated by the above methods, especially if they are dominated by statistical fluctuations and not by systematic errors. For a slightly more complete description, see the Wiki article .
Sensitivity
Sensitivity and signal-to-noise are synonymous for our purposes. There can be various sources of noise:- a) Read noise,
 from the detector
from the detector - This is a constant for a given detector - it occurs due to errors in the reading out of the CCD chip.
- b) Dark current,
 in the detector
in the detector - This is the noise that remains in the detector even when all sources are removed. It is due to thermal motions of electrons within the detector electronics, and can be reduced by lowering the CCD temperature.
- c) Photon shot noise,
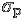
-
Photons follow Poisson statistics. Poisson statistics reduce to Gaussian statistics when the photon rate is high. The standard deviation of the fluctuations in the number of photons received per unit time is equal to the square root of the mean number of photons received per unit time (that's a mouthful!) As an example, if the slit lets through N = 2500 photons per second on average, then the number of photons that actually go through it and land on the detector in any 1 second will fluctuate about 2500 with a standard deviation of
 .
.In other words, if you count the photons allowed through in 1 second and repeat the experiment several times, and plot a histogram of the numbers that you get, then the distribution of these numbers will be approximately Gaussian. The peak of this Gaussian would be at N = 2500 photons per second and the width would be called the shot noise,
 photons per second.
photons per second.
Increasing the slit width in a spectrometer experiment increases the photon rate, i.e. N and correspondingly increases the shot noise, given by .
.
All these sources of noise (and any other contributions to it that you think are important) add in quadrature:
The signal-to-noise is then defined as:
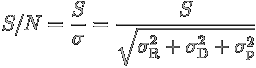
Effect of changing the exposure time
Increaasing the exposure time for a fixed slit width increases the number of photons collected. Since the photon noise scales with the number of photons collected, increasing it can make the photon noise dominant over all other sources of noise
.
In this case, the signal-to-noise simply increases as ![]() , and longer exposures are better. Real telescopes work by taking many frames of a fixed exposure and then
adding them together, since they can't deal with too many photons in one exposure without getting saturated (the saturation limit of the detector we are using in Ay 16 is ~ 65000 counts).
, and longer exposures are better. Real telescopes work by taking many frames of a fixed exposure and then
adding them together, since they can't deal with too many photons in one exposure without getting saturated (the saturation limit of the detector we are using in Ay 16 is ~ 65000 counts).
Resolution
The spectrograph convolves the natural width of the lines with its own response function. The most important contributor to the reponse function of a spectrograph is the slit width.
A slit can be modelled as a top hat (rectangular function), which lets light through only in a small interval, ![]() .
The observed line profile is a convolution of the slit profile
(actually, of the diffraction pattern from the slit, but we will ignore that for this discussion)
with the true line profile, which itself may be broadened by the effects of thermal Doppler shifts,
unresolved rotation, and natural line broadening, in general.
.
The observed line profile is a convolution of the slit profile
(actually, of the diffraction pattern from the slit, but we will ignore that for this discussion)
with the true line profile, which itself may be broadened by the effects of thermal Doppler shifts,
unresolved rotation, and natural line broadening, in general.
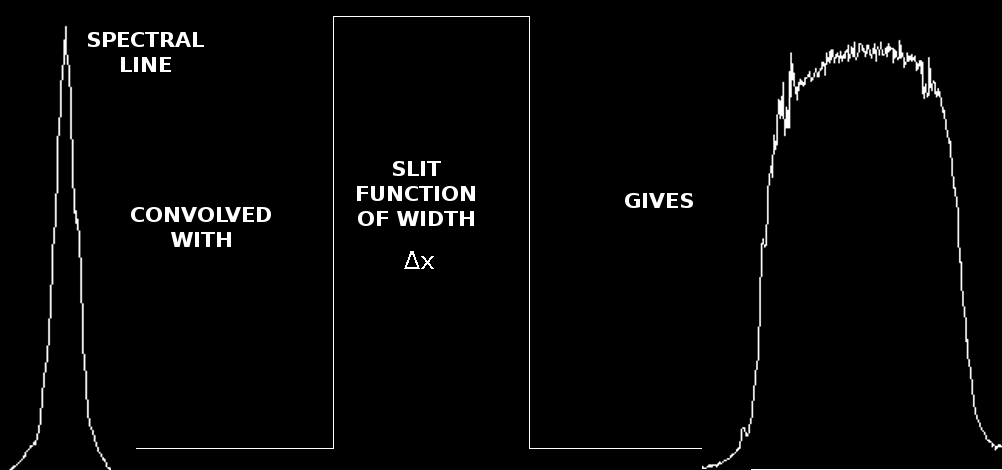
The effect of the slit on the observed spectrum. To the left is a line observed with a very narrow slit, and to the right, the same line has been observed with a much broader slit. These data were taken on March 2, 2010 by one of the groups during their solar lab. The jagged edges in the last image are due to noise - the exposure was much shorter and the effect of increasing the slit width did not compensate completely.
Therefore, using a broader slit would let more light through (as can be seen by the discussion of sensitivity above) and improve the signal-to-noise, but it would result in the loss of resolution, as the lines become broader. There is thus a trade-off between the two, and the slit width used will depend upon the needs of the experiment.
The convolution of two Gaussian Functions
The convolution
of two functions, f(x) and g(x) is defined as
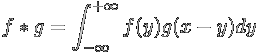
A Gaussian function centered at x = 0 is defined as

Consider two Gaussian functions given by
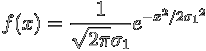 ,
and
,
and
 .
.
Then their convolution is given by
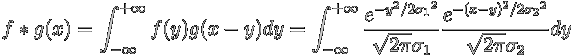
Now the exponents of the exponentials add to (the negative of)
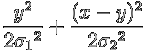





![]() ,
,
where  ,
and
,
and ![]() .
.
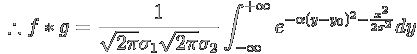
Since ![]() is independent of y, it acts as a constant for the y-integral,
which can now be performed. We use the standard formula
is independent of y, it acts as a constant for the y-integral,
which can now be performed. We use the standard formula
 ,
, ,
, Therefore, the convolution of two Gaussian functions is another Gaussian function, whose variance is the sum of the squares of the variances of the individual functions.
The working of a diffraction grating
Before starting to look into how a diffraction grating works, make sure you understand diffraction due to a single slit. A very good resource is the hyperphysics website (go to "Light and Vision", then "single slit"). A grating is a large number of slits arranges parralel to each other on a piece of glass. There are two kinds of gratings: transmission and reflection gratings. We shall consider a transmission grating here, though the results apply to a reflection grating as well.
Consider N slits, each of width a and height b, with center-to-center separation d. Let these be illuminated by a collimated beam of light (i.e. plane waves with straight wavefronts: this can be achieved by placing a source of light at the focus of a lens, for example, and shining the resulting parallel beam on to the grating). The light waves passing through the slits will form an interference pattern on the screen.
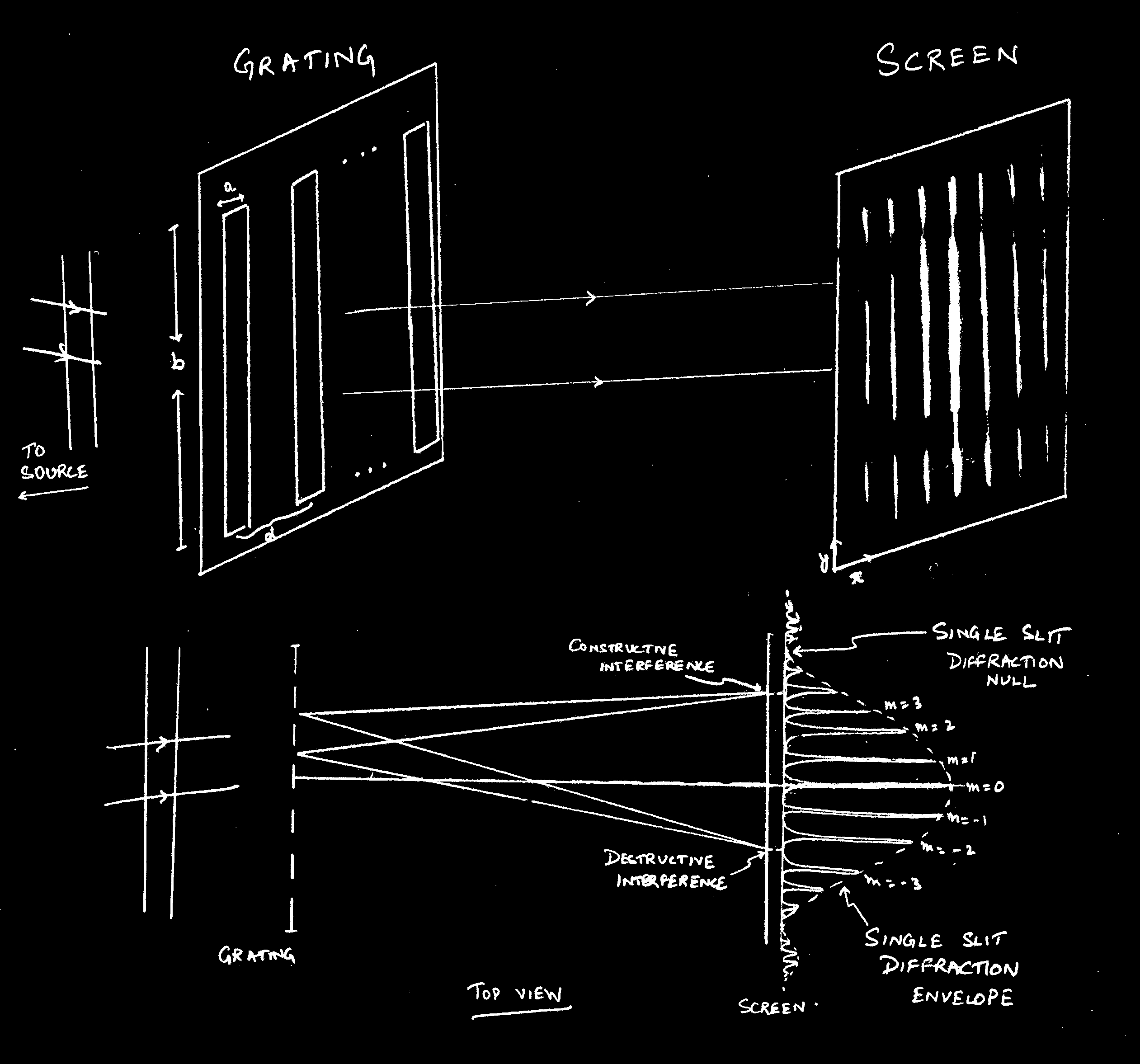
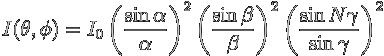 ,
, where
Here λ is the wavelength of the light and ![]() is the intensity from a
single slit in the absence of diffraction.
is the intensity from a
single slit in the absence of diffraction.
Note that the first term,  depends only on θ, and therefore describes variations in the vertical
direction, while the other two terms depend only on ϕ, and therefore
describe variations in the horizontal, or ϕ-direction.
depends only on θ, and therefore describes variations in the vertical
direction, while the other two terms depend only on ϕ, and therefore
describe variations in the horizontal, or ϕ-direction.
 term into
term into
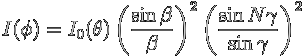 , with
, with

Check for yourself that for N = 1 this formula reduces to the single slit diffraction pattern.
Now since ![]() (from the definitions of γ and
(from the definitions of γ and ![]() ),
the first term
),
the first term
 varies more slowly than the
second term and represents the single slit diffraction pattern.
This creates an envelope (labelled "single slit diffraction envelope"
in the figure).
varies more slowly than the
second term and represents the single slit diffraction pattern.
This creates an envelope (labelled "single slit diffraction envelope"
in the figure).
Note than 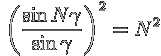 whenever
whenever ![]() . These are maxima of the second term (plot it!)
Substituting the expression for γ from above, this yields
the grating equation:
. These are maxima of the second term (plot it!)
Substituting the expression for γ from above, this yields
the grating equation:
The dispersive power of the grating is defined as its ability to separate light of different wavelengths into different directions:
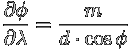
Finally, when the incident light is at an angle ![]() to the normal
to the grating, the grating equation gets modified to:
to the normal
to the grating, the grating equation gets modified to:
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge MA 02138, USA
laskar :a:t: fas.harvard.edu Office: A-107 +1-617-495-5989