

Next: Dirty Image
Up: Basics in Imaging, Deconvolution
Previous: Introduction
Weighting in the imaging process is important in order to improve
the dynamic range and the fedility of a final aperture synthesized image.
The ATNF's Users Guide gives a thorough discussion and description in
both sampling density weighting and sensitivity weighting.
The description of the weighting methods is relevant to the
SMA users. For the SMA users convenience, we duplicate their
discussion interleaving with some comments for the SMA specifications.
Each visibility sample is given a weight in the imaging step. This
weighting can be used to account for differences in the density of
sampling in different parts of the u-v plane, or to account
for different noise variances in different samples, or to improve
sensitivity to extended objects, etc. Here we briefly review some
weighting schemes:
- Natural weighting
- This gives constant weights to all
visibilities (or, more strictly,
inversely proportional to the noise variance of a visibility). This weighting
gives optimum point-source sensitivity in an image. However the synthesised
beam-shape and sidelobe levels are usually poor.
- Uniform weighting
- This gives a weight inversely proportional to
the sampling density function. This form of weighting minimizes the sidelobe
level. However the noise level can be a factor of 2 worse than natural
weighting.
- Super- and sub-uniform weighting
- Uniform weighting computes the
sampling density function on a grid that is the same size as the
gridded u-v plane. This results in the synthesised beam sidelobes
being minimized over the same field-of-view as the region being
image. Surprisingly, making the field-of-view very large (bigger than
the primary beam size) or very small (comparable to the synthesised beam)
both cause uniform weighting to reduce to natural weighting.
Super- and sub-uniform weighting decouple the weighting from the field size
being imaged. Instead, the sidelobes in the synthesised image are minimized
over some arbitrary field size, with this field being either smaller or
larger than the field being imaged (for super- or sub-uniform weights
respectively).
- Robust weighting
- Uniform weighting (including super- and sub-uniform
weighting) minimizing sidelobes, whereas natural weighting minimizes
the noise level. Robust weighting provides a compromise between the two,
doing so in an optimal sense (similar to Wiener optimisation).
See Dan Briggs' thesis for more information
(Dan Briggs' dissertations).
- Tapering
- In signal processing theory, the optimum way to
detect a signal of known form, which is buried in noise, is to
convolve that signal with a ``matched filter''. This filter has
an impulse response which is just the reverse of the form of
the signal that is being detected. Applying this principle to
detecting sources in radio interferometry, the optimum
weighting for detecting a Gaussian source is to weight the
visibility data by a Gaussian. This is often called `tapering'.
Using a Gaussian weight will significantly increase the detectability
of an extended source. However it also degrades the resolution. Gaussian
weighting can be combined with any of the above weighting schemes to
achieve some form of balance between sidelobes and sensitivity.
Miriad gives good control over the visibility
weighting schemes, via three parameters and one option.
- fwhm controls tapering of the data.
Unlike AIPS, this taper is specified in the image domain,
in arcseconds. If you are interested in features of a particular
angular size, then the signal-to-noise ratio in the
resultant dirty image is optimised for these features if the taper FWHM is
the same as the source FWHM (or source scale size).
- sup is used to control super- and sub-uniform weighting.
The sup parameter indicates the region of the dirty beam
(centred on the beam centre) where sidelobes are to be suppressed or
minimized. Like the fwhm parameter, the sup parameter is
given in arcseconds. The weights that invert
calculates are
optimal, or near optimal, in a least-squares sense to minimizing
the sidelobes in the specified region of the beam. Although the
sidelobe suppression region is not a direct control of resolution and
signal-to-noise ratio, it does have an effect on these
characteristics.
Suppressing sidelobes over the entire field of the dirty beam
corresponds to uniform weighting - that is, we get uniform weighting if
sup is set to the field size of the dirty beam; this is the
default. Alternately making no attempt to
suppress sidelobes (sup=0) corresponds to natural weighting.
Increasing sup from 0 to the field size results initially in an
improvement in resolution until the value of sup is approximately
equal to the best resolution. Increasing sup beyond this results
in a slow degradation in resolution. The noise level varies in
a less regular way with sup. Apart from saying that sup=0
(natural weighting) gives the optimum signal-to-noise ratio, it is not
possible to generalise. However the noise level will be no worse than
a factor of a few from the optimum.
The default value for sup is the field size (i.e. uniform
weighting).
- robust: In Miriad, robust weighting is parameterized
by a ``robustness'' parameter. Values less than about -2 correspond
essentially to minimizing sidelobe levels only, whereas values greater than
about +2 just minimizing noise. A value of about 0.5
gives nearly the same sensitivity as natural weighting, but with
a significantly better beam.
- options=systemp: The basic weight of a visibility (the weight used
for natural weighting, or the weight used for a point in determining the
local sampling density function) is ideally
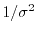 , where
, where 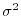 is
the noise variance of a visibility. For no Tsys information given,
invert
normally assumes the
noise variance is inversely proportional to the integration time
(
is
the noise variance of a visibility. For no Tsys information given,
invert
normally assumes the
noise variance is inversely proportional to the integration time
(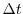 ) and the bandwidth (
) and the bandwidth (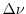 ) of a
visibility. However SMA data
loaded with Miriad task smalod
contains antenna-based Tsys
measurements and Miriad can calculate
) of a
visibility. However SMA data
loaded with Miriad task smalod
contains antenna-based Tsys
measurements and Miriad can calculate 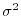 using the formula below:
using the formula below:
where
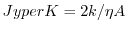 and A is antenna area,
and A is antenna area,
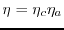 is an efficiency, k is Boltzmans constant.
is an efficiency, k is Boltzmans constant.
The options = systemp can instruct invert
to compute the basic
weights using 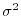 .
The calculation assumes that the parameters A,
.
The calculation assumes that the parameters A, 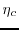 and
and
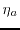 are
constant across the array
and the sky, i.e.
are
constant across the array
and the sky, i.e. 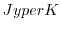 is assumed to be constant.
For optimizing the sensitivity of the final synthesized image, the
relative weights derived from options = systemp
need to be applied.
is assumed to be constant.
For optimizing the sensitivity of the final synthesized image, the
relative weights derived from options = systemp
need to be applied.


Next: Dirty Image
Up: Basics in Imaging, Deconvolution
Previous: Introduction
Jun-Hui Zhao (miriad for SMA)
2012-07-09
![]() .
The calculation assumes that the parameters A,
.
The calculation assumes that the parameters A, ![]() and
and
![]() are
constant across the array
and the sky, i.e.
are
constant across the array
and the sky, i.e. ![]() is assumed to be constant.
For optimizing the sensitivity of the final synthesized image, the
relative weights derived from options = systemp
need to be applied.
is assumed to be constant.
For optimizing the sensitivity of the final synthesized image, the
relative weights derived from options = systemp
need to be applied.