
In the first million years of the universe, however, there is a remarkable occurance in which the density perturbations in the universe behave in part as sound waves. This gives rise to marvelous structure in the anisotropies of the microwave background, notably a characteristic angular scale and the famous acoustic (or Doppler, or Sakharov) peaks.
These same features are predicted to create a small residual imprint in the clustering of matter today. This page is an attempt to illustrate how this occurs.
Let's consider what happens to a point-like initial perturbation. In other words, we're going to take a little patch of space and make it a little denser. Of course, the universe has many such patchs, some overdense, some underdense. We're just going to focus on one. Because the fluctuations are so small, the effects of many regions just sum linearly.
The relevant components of the universe are the dark matter, the gas (nuclei and electrons), the cosmic microwave background photons, and the cosmic background neutrinos.
In the standard theory, the initial perturbations are adiabatic, so all of the species are perturbed the same fractional amount. [Well not quite: the photons and neutrinos, being ultrarelativistic, have an energy perturbation 4/3 bigger than the dark matter and gas. I've removed that scaling.]
One should remember thoughout that the densities of all species are very close to smooth. We are only describing a tiny perturbation on this smooth background. Here's the initial perturbation. Black is dark matter, blue is gas, red is photons, green is neutrinos. [The small differences are just an artifact of the Fourier transform.]

Now what happens?
The neutrinos don't interact with anything and are too fast to be bound gravitationally, so they begin to stream away from the initial perturbation.
The dark matter moves only in response to gravity and has no intrinsic motion (it's cold dark matter). So it sits still. The perturbation (now dominated by the photons and neutrinos) is overdense, so it attracts the surroundings, causing more dark matter to fall towards the center.
The gas, however, is so hot at this time that it is ionized. In the resulting plasma, the cosmic microwave background photons are not able to propagate very far before they scatter off an electron. Effectively, the gas and photons are locked into a single fluid. The photons are so hot and numerous, that this combined fluid has an enormous pressure relative to its density. The initial overdensity is therefore also an initial overpressure. This pressure tries to equalize itself with the surroundings, but this simply results in an expanding spherical sound wave. This is just like a drum head pushing a sound wave into the air, but the speed of sound at this early time is 57% of the speed of light!
The result is that the perturbation in the gas and photon is carried outward:

We're plotting density times the square of radius so that the area under the curve is the mass in the perturbation. Like all expanding spherical waves, the density itself is dropping quickly because the energy is being spread over a large area. By density, we mean the fractional density perturbation in each species. In other words, if the curves are the same height, then the fractional perturbation is the same in all species. This does not include the fact that there is 5 times more dark matter than gas or that the density of the photons and neutrinos is changing relative to the gas and dark matter.
The units of radius is in megaparsecs (Mpc) as it would be measured today. The universe is expanding and so two given points today were separated by less distance in the past. This means that it would take light less time to travel from one to the other, so in the first million years after the Big Bang, the wave can travel a distance that today is far more than one million light-years. It is easier to understand what's happening if one focuses on what would be seen by observers moving with the expanding universe. That's what our choice of distance convention does. Astronomers call this convention the comoving coordinate system.
As time goes on, the spherical shell of gas and photons continues to expand. The neutrinos spread out. The dark matter collects in the overall density perturbation, which is now considerably bigger because the photons and neutrinos have left the center. Hence, the peak in the dark matter remains centrally concentrated but with an increasing width. This is generating the familiar turnover in the cold dark matter power spectrum.
Where is the extra dark matter at large radius coming from? The gravitational forces are attracting the background material in that region, causing it to contract a bit and become overdense relative to the background further away.

The expanding universe is cooling. Around 400,000 years, the temperature is low enough that the electrons and nuclei begin to combine into neutral atoms. The photons do not scatter efficiently off of neutral atoms, so the photons begin to slip past the gas particles. This is known as Silk damping (ApJ, 151, 459, 1968).
The sound speed begins to drop because of the reduced coupling between the photons and gas and because the cooler photons are no longer very heavy compared to the gas. Hence, the pressure wave slows down.
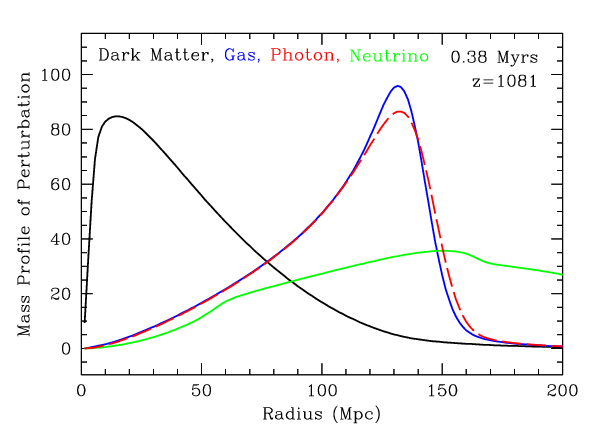
This continues until the photons have completely leaked out of the gas perturbation. The photon perturbation begins to smooth itself out at the speed of light (just like the neutrinos did). The photons travel (mostly) unimpeded until the present-day, where we can record them as the microwave background (see below).
At this point, the sound speed in the gas has dropped to much less than the speed of light, so the pressure wave stalls.

We are left with a dark matter perturbation around the original center and a gas perturbation in a shell about 150 Mpc (500 million light-years) in radius.
As time goes on, however, these two species gravitationally attract each other. The perturbations begin to mix together. More precisely, both perturbations are growing quickly in response to the combined gravitational forces of both the dark matter and the gas. At late times, the initial differences are small compared to the later growth.

Eventually, the two look quite similar. The spherical shell of the gas perturbation has imprinted itself in the dark matter. This is known as the acoustic peak.
The acoustic peak decreases in contrast as the gas come into lock-step with the dark matter simply because the dark matter, which has no peak initially, outweighs the gas 5 to 1.
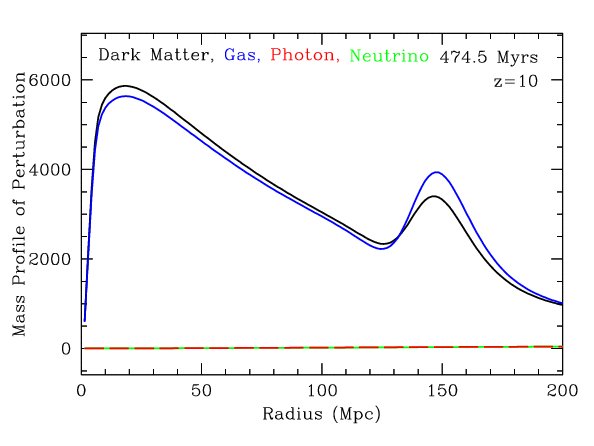
Remember, however, that we have been plotting the mass profile (density times radius squared). The density profile is much steeper, so that the peak at 150 Mpc is much less than 1% of the density near the center.

At late times, galaxies form in the regions that are overdense in gas and dark matter. For the most part, this is driven by where the initial overdensities were, since we see that the dark matter has clustered heavily around these initial locations. However, there is a 1% enhancement in the regions 150 Mpc away from these initial overdensities. Hence, there should be an small excess of galaxies 150 Mpc away from other galaxies, as opposed to 120 or 180 Mpc. We can see this as a single acoustic peak in the correlation function of galaxies. Alternatively, if one is working with the power spectrum statistic, then one sees the effect as a series of acoustic oscillations.
Here's an animation (1.6 MB) of this whole process.
Here's the same animation (1.6 MB), but in density.
There are two differences between the CMB and the gas/dark matter that one should keep in mind, however:
The cosmology used here is Omega_matter = 0.30, Omega_baryon = 0.049, h = 0.7, with massless neutrinos.
 Back to Steward Observatory Home Page
Back to Steward Observatory Home Page