 |
Normally, an observation track includes a bandpass scan on a small planet or a strong quasar. As long as the visibility data on each channel gives adequate S/N, one can solve for antenna-based bandpass solutions using smamfcal. Here is an exmaple for solving for bandpass based on observations of the Jupiter's moon, Callisto.
Task: smamfcal
vis = gc_rx1.lsb.tsys % input data with Tsys correction
and bad data that are flagged.
select = source(call*) % here select a calibrator with
wildcard call* = callisto
refant = 3
interval = 100 % time interval for bandpass solutions
weight = 2 % the channel visibility is normalized
% by the average of channels specified
% by the inner 75% of each "spectral
chunk";
The above setup of smamfcal for bandpass is given using the calibrator Callisto. The solutions can be checked with smagpplt:
smagpplt% inp
Task: smagpplt
vis = gc_rx1.lsb.tsys % input file with bandpass table
device = /xs % x-window device
log =
yaxis = amp,phase % displays amplitude and phase
options = bandpass,opolyfit % bandpass; bandpass solutions
will be replaced by the
polynomial fit
polyfit = 5 % the 5th order polynomial is
used in the least square fit.
nxy = 2,4 % page setup: 2 in row and 4 in
column.
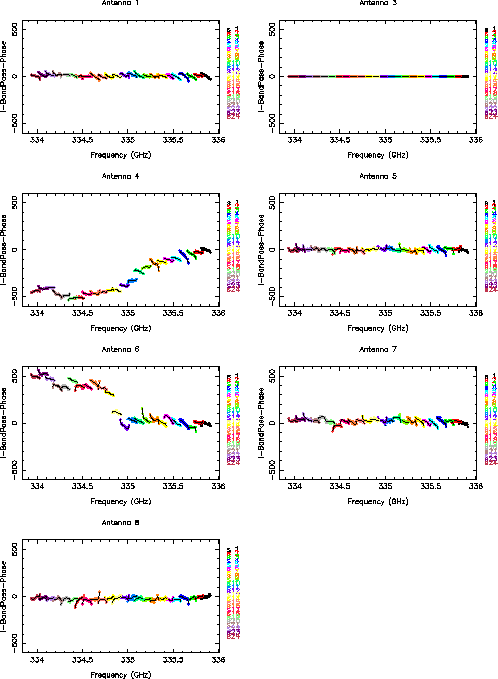
The solutions for amplitude and phase are shown in (Figs. 3.1 and 3.2). The ripples in amplitude shown in the antenna based solutions across the 2 GHz band needs to be corrected. The data of antenna 2 is relatively noisy and poor. Antenna 2 has been removed before solving for bandpass. Antenna 4 shows a large delay across all the chunks. Antenna 6 shows a big phase jump between the first 3 blocks (12 chunks) and the next 3 blocks. The phase solutions of the antennas are with respect to the reference antenna 3. The errors must be removed. This is particularly important for continuum data which is an average of the spectral data. Also the bandpass solution appears to be little noisy and one can fit a polynomial to the solutions. The solid curves are the fitted version of the bandpass solutions. If the polynomial fit is satified, one can run smagpplt by re-setting the options to options = bandpass,opolyfit with other parameters remaining the same. Then the bandpass solutions are replaced by the polynomial fit. Note that the options of opolyfit will replace the original solution. We encourage users to try these parameters. If mistakes occur, one can always re-run smamfcal to calculate the solutions again.
 |
 |